Fall 2021 Issue
Photo credit: Imperial College London
Mathematics has been used for nearly 100 years to gain insight into disease spread
and control-measures. The CDC (Center for Disease Control) and WHO (World Health Organization)
use mathematical models to describe how a disease spreads through a population. These
models give a picture of how diseases propagate through a population and allow them
to assess strategies to control or prevent diseases. Questions such as how many will
be infected, how long will epidemics last and how will individuals/populations be
affected can be answered. These models impact policies to control/end an epidemic
such as treatment methods, vaccinations and prevention strategies.
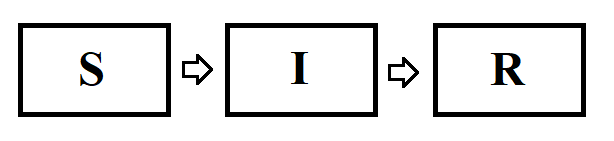
SIR Model
William O. Kermack and A.G. McKendrick observed (1920s) that a population that is exposed to an infection can be divided into three categories– Susceptible (S), Infected (I) and Recovered (R), creating an SIR model. The SIR model is a compartmental model (Figure 1), where each individual falls in one of the three compartments. Susceptible individuals encounter an infectious individual and can contract the disease (with some probability). Infectious individuals are capable of infecting susceptible individuals. As the infected population increases, susceptible will decrease. Recovered class are those that have been infected and are now removed (immune or deceased). Each group can be represented by a differential equation modeling the rate of change of each group. The solution of the Kermack-McKendrick equations estimate what fraction of the population is in each group at a given time. These solutions are used to predict possible outbreaks and ways to control them.
In the simple SIR model population remain constant. There are many modifications of the SIR model, including those that include births and deaths. A model could include an exposed period where an individual has no clinical signs of the disease but is infectious (SEIR). There are other models whereupon recovery there is no immunity (SIS model) or where immunity lasts only for a short period (SIRS). The type of compartmental model used depends on the dynamics of the disease. Models also can include reduction strategies, such as quarantine and vaccinations.
Since their beginning, mathematical models have played a prominent role in transforming public health care. Governments, health organizations, scientists and hospitals depend heavily on models to deal with the onslaught of issues that arise out of medical problems.
Modeling COVID-19
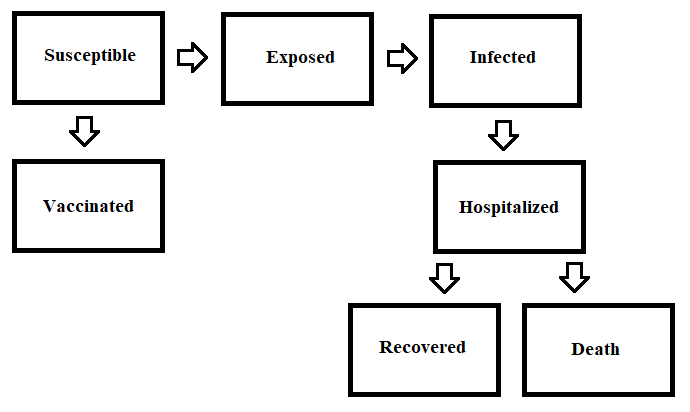
Several models have emerged in modeling the present coronavirus. These models have been used to determine transmissibility, calculate the expected number of cases and how quickly the disease might spread, along with determining the effect quarantining, social distancing measures and vaccinations would have on reducing the number of cases. They aid health services in determining the best strategies in implementing these reduction measures and effect immediate policymaking. Questions like who should get the vaccine first to prevent the most cases can be answered. Models need to balance realism and complexity. Good data needs to be available to make accurate models. A COVID-19 model would need an exposed class, making an SEIR the appropriate model. The SEIR model can add two compartments, vaccinated population and hospitalized population to create a more realistic model. The hospitalized individuals could either recover or die. See Figure 2 for how the population can move through these compartments.
The Future of Mathematical Modeling
As new diseases emerge and old diseases reemerge, mathematics will continue to play an important role in policymaking. The more we learn about diseases and gain data, the more accurate models and hence predictions can be made. Many diseases being modeled are life-threatening. Running real-life experiments is not ethical. Mathematics is our best tool to fight epidemics.